PPO and ACKTR Methods in RL

Introduction

Vanilla Policy Gradient methods are high variance and can lead to convergence issues as policies might change too drastically with certain gradient steps. Trust Region Policy Optimisation (TRPO) is a method that uses natural gradients to take the largest step while ensuring improvement in policy performance. Natural policy gradient involves a second-order derivative matrix which makes it not scalable for large scale problems as calculating the inverse of this matrix is computationally very costly.

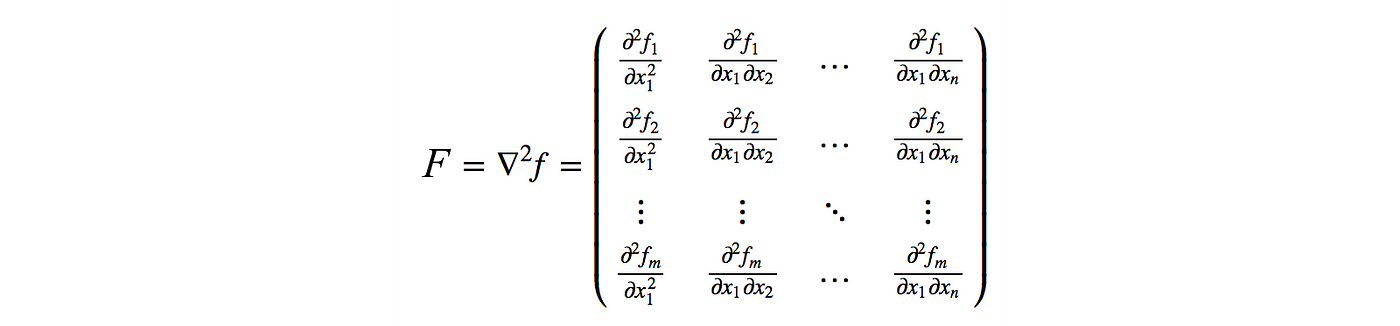
There are two approaches to address this problem:

• Approximate some calculations involving the second order derivative and its inverse to lower the computational complexity, or
• Make the first order derivative solution, like the gradient descent, closer to the second-order derivative solution by adding soft constraints.

Proximal Policy Optimisation (PPO)

PPO is an on-policy algorithm. It is a family of first-order methods that use a few other tricks to keep new policies close to old. PPO methods are significantly simpler to implement, and empirically seem to perform at least as well as TRPO. There are two primary variants of PPO: PPO-Penalty and PPO-Clip.

• PPO-Penalty approximately solves a KL-constrained update like TRPO, but penalizes the KL-divergence in the objective function instead of making it a hard constraint, and automatically adjusts the penalty coefficient over the course of training so that it’s scaled appropriately.

• PPO-Clip doesn’t have a KL-divergence term in the objective and doesn’t have a constraint at all. Instead relies on specialized clipping in the objective function to remove incentives for the new policy to get far from the old policy.

PPO with Adaptive KL Penalty

It changes the objective function to include the KL divergence as a soft constraint

$maximize_{\theta} E_{t}[ \frac{\pi_{\theta(a_t | s_t)}}{\pi_{\theta_{old}(a_t | s_t)}}A_t] \space - \space \beta D_{KL}(\pi_{\theta_{old}}(.|s)||\pi_{\theta}(.||s))]$

$\beta$ controls the weight of the penalty. It penalizes the objective if the new policy is different from the old policy.

PPO with Clipped Objective

There are 2 policy networks, the first is the current policy that we want to improve and the second is the policy we last used to collect samples.

$\theta_{k+1} = argmax_{\theta} E_{s,a \sim \pi_{\theta_{k}}} [L(s,a,\theta_{k}, \theta)]$

typically we take multiple steps of SGD to maximise this objective. Here L is given by

$L(s,a,\theta_{k}, \theta) = min( \frac{ \pi_{\theta}(a|s)}{ \pi_{\theta_{k}}(a|s)} A^{\pi_{\theta_k}}(s,a), clip( \frac{ \pi_{\theta}(a|s)}{ \pi_{\theta_{k}}(a|s)} , 1- \epsilon, 1 + \epsilon) A^{\pi_{\theta_k}}(s,a)$

where $\epsilon$ which is a hyperparameter that decides how far away the new policy is allowed to go from the old policy. We can also write the equation as

$L(s,a,\theta_{k}, \theta) = min( \frac{ \pi_{\theta}(a|s)}{ \pi_{\theta_{k}}(a|s)} A^{\pi_{\theta_k}}(s,a), g(\epsilon , A^{\pi_{\theta_k}}))$

where

$g(\epsilon , A^{\pi_{\theta_k}}) = (1+ \epsilon) A^{\pi_{\theta_k}} \quad if A \ge 0$

$g(\epsilon , A^{\pi_{\theta_k}}) = (1- \epsilon) A^{\pi_{\theta_k}} \quad if A \lt 0$

Advantage is positive: Suppose the advantage for that state-action pair is positive, in which case its contribution to the objective reduces to

$L(s,a,\theta_{k}, \theta) = min( \frac{ \pi_{\theta}(a|s)}{ \pi_{\theta_{k}}(a|s)}, (1+ \epsilon))A^{\pi_{\theta_k}}$

Because the advantage is positive, the objective will increase if the action becomes more likely that is, if $\pi_{\theta}(a|s)$ increases. But the min in this term puts a limit to how much the objective can increase. Once $\pi_{\theta}(a|s) > (1+\epsilon) \pi_{\theta_k}(a|s)$ , the min kicks in and this term hits a ceiling of $(1+\epsilon) A^{\pi_{\theta_k}}(s,a)$ . Thus: the new policy does not benefit by going far away from the old policy.

Advantage is negative: Suppose the advantage for that state-action pair is negative, in which case its contribution to the objective reduces to

$L(s,a,\theta_{k}, \theta) = max( \frac{ \pi_{\theta}(a|s)}{ \pi_{\theta_{k}}(a|s)}, (1- \epsilon))A^{\pi_{\theta_k}}$

Because the advantage is negative, the objective will increase if the action becomes less likely—that is, if $\pi_{\theta}(a|s)$ decreases. But the max in this term puts a limit to how much the objective can increase. Once $\pi_{\theta}(a|s) < (1-\epsilon) \pi_{\theta_k}(a|s)$, the max kicks in and this term hits a ceiling of $(1-\epsilon) A^{\pi_{\theta_k}}(s,a)$. Thus, again: the new policy does not benefit by going far away from the old policy.

Exploration vs Exploitation

PPO trains a stochastic policy in an on-policy way. This means that it explores by sampling actions according to the latest version of its stochastic policy. The amount of randomness in action selection depends on both initial conditions and the training procedure. Over the course of training, the policy typically becomes progressively less random, as the update rule encourages it to exploit rewards that it has already found. This may cause the policy to get trapped in local optima.

Psuedocode

ACKTR

ACKTRK is:

• A Policy Gradient method with the trust region optimization,
• An actor-critic architecture similar to A2C: one deep network to estimate the policy and another network to estimate the advantage function,
• Apply the Kronecker-factored approximation to optimize both actor and critic (will be explained next),
• Keep a running average of the curvature information.

The approximation happens in 2 stages; First the rows and columns of the fisher information matrix are divided into groups where a group consists of weights belong to a single layer. These blocks are then approximated as Kronecker products between much smaller matrices. In the second stage, this matrix is further approximated as having an inverse which is either block-diagonal or block-tridiagonal.

K-FAC calculates the derivative of L relative to model parameters w in a deep network layer, instead of the whole model.

$\nabla_{w}L = (\nabla_{s}L)a^T$

$F = E_{p(\tau)}[\nabla_{\theta}log \space\pi(a_t|s_t) \space (\nabla_{\theta}log \space\pi(a_t|s_t))^T]$

$F_l = E[vec\{\nabla_{w}L \} \space vec\{\nabla_{w}L \}^T]$

$F_l = E[aa^T \times \nabla_{s}L(\nabla_{s}L)^T] \approx E[aa^T] \times E[\nabla_{s}L(\nabla_{s}L)^T]$

$\hat{F_l} := A \times S$

where $A$ is defined as $E[aa^T]$ and $S$ is defined as $E[\nabla_{s}L(\nabla_{s}L)^T]$.
here we use $\times$ to denote the outer product.

Using $(P \times Q)^{-1} = P^{-1} \times Q^{-1}$ and $(P \times Q)vec(T) = PTQ^T$

The updates to W for each layer become:

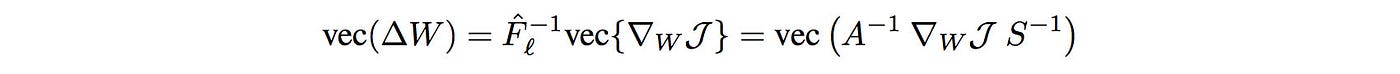
So to compute the parameter changes for each layer, we find the inverse of A and S below:

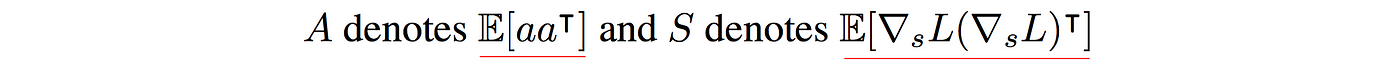
We update the network layer-by-layer. Each calculation involves nodes in each layer only. Consider the number of nodes in each layer is in thousand or hundred ranges, rather than millions for the whole network. This is much manageable and K-FAC significantly reduces the computational complexity.

Summary

ACKTR

• uses trust-region optimization to improve the convergence.
• approximates the parameter updates with K-FAC for both actor and critic. It reduces the computational complexity closer to first-order optimizers (like the common stochastic gradient descent).
• maintains running averages to reduce variance in the K-FAC calculation. This allows K-FAC to use less sample than TRPO to approximate the inverse of F accurately.

ACKTR scales better with larger deep network models. It solves tasks in continuous control space with raw pixel observation which TRPO cannot handle.